The level of measurement is a classification that describe the nature of information within the values assigned to the variables (https://en.wikipedia.org/wiki/Level_of_measurement).
It is important for researchers to understand the different level of measurement. To know the level of measurement helps us to decide what statistical analysis is appropriate for the variables, and how to interpret the data form variables. The four different level of measurements are:
1) Nominal - In this level of measurement, words, letters, numbers, or symbols can be used to the attributes of what we want to measure. The numerical values just "name" for the attributes to classify the data.
2) Ordinal - This level of measurement, the attributes can be ordered relationship among variables (1st, 2nd, 3rd, etc.). Distances between attributes do not have any meaning.
3) Interval - In this level of measurement, the distance between attributes does have meaning. The distances between each interval on the scale are equivalent along the scale from low level to high level. We can compute an average of an interval variable.
4) Ratio - For the ratio level of measurement, it has equal interval along the scale and has a meaningful value of "zero".

Sources of Error
In general, no set of data is perfect. the data contains some margin of error. There are three basic types of error: human error, systematic error, and random error.
1) Human errors - This kind of error occurs when researcher simply makes a mistake such as misreading the instrument.
2) Systematic errors - This type of error is caused by the way the experiment designed or conducted. It is introduced by inaccurate observation or measurement process. This type of error can be reduced by very carefully with standardized procedures..
3) Random errors - Random errors are unpredictable and are chances variations in the measurements. When a measurement is repeated, it will generally provide a different values from the previous measurement. This kind of error lead to measurable values being inconsistent when repeated measurements of a constant attributes or quantity. This kind of error will not be controlled.
For scale development, every measurement involves some error. Measurement error may be random or systematic. The random error is an element that must be considered in all measurement. Random error can never completely eliminated but one should seek to minimize it as much as possible. Random errors limit the degree of precision in estimating the true score from observed score which lead to decrease reliability. Systematic error affects the true scores of all subjects which lead to decrease the validity of the measure (Waltz, Strickland, & Lenz., 2010).
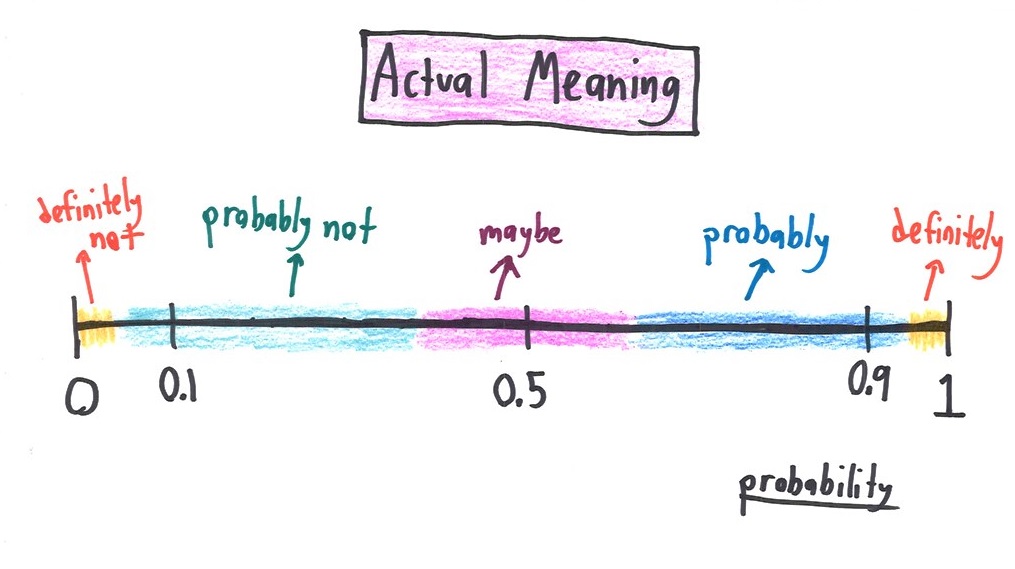
Probability
Probability is the extent to which something is probable, which is expressed as a number between 0 and 1. An event with a probability of 1 can be indicated a certainty, while an event with a probability of 0 can be indicated an impossible.
In its simplest form, probability can be calculated as:
p(a) = p(a)/[p(a) + p(b)]
Probability theory applies precise calculations to quantify uncertain measures of random events.
Reference:
Waltz, C. F., Strickland, O. L., & Lenz, E. R. (2010). Measurement in nursing and health
research (4th ed.). New York: Springer Publishing.
No comments:
Post a Comment