Classical test theory (CTT) and
Item Response Theory (IRT) are widely used as statistical measurement
frameworks. CTT is approximately 100 years old, and still remains commonly used
because it is appropriate for certain situations. Although CTT has served the
measurement community for most of this century, IRT has witnessed an
exponential growth in recent decades. IRT is generally claimed as an
improvement over CTT.
Classical Test theory (CTT)
CTT is a
theory about test scores that introduces three concepts - test score (observed
score), true score, and error score. A simple linear model is postulated
linking the three concepts as the basic
formulation as follow:
O
(observed score) = T (true score) + E (random error)
The assumptions in CTT model are that
(1)
true scores and error scores are uncorrelated,
(2)
the average error score in the population of respondent is zero,
(3)
error scores on parallel tests are uncorrelated.
CTT
is assumed that measurements are not perfect. The observed score for each
person may differ from their true ability because the true score influenced by
some degree of error. All potential sources of variation existing in the
process of testing either external conditions or internal conditions of person are
assumed to have an effect as random error. It is also assumed that random error
found in observed scores are normally distributed and uncorrelated with the
true scores. As this equation, minimizing the error score and reducing the
difference between observed and true scores is desirable to yield more true
score answers.
The
CTT models have linked test scores to true scores rather than item scores to
true scores. Scores obtained from CTT applications are entirely test dependent.
In addition, the two statistics (item difficulty and item discrimination) are
entirely dependent on the respondent sample taken the test, as well as reliability
estimates are dependent upon test scores from beta samples.
Advantage and implication of CTT
The
main advantage of CTT is its relatively weak theoretical assumptions, which
make CTT easy to meet real data and modest sample size, and apply in many
testing situations. CTT is useful for assessing the difficulty and discrimination
of items, and the precision with which scores are measured by an examination.
In
application, the main purpose of CTT within
psychometric testing is to recognise and develop the reliability of
psychological tests and assessments.
1)
True scores in the population are assumed to be measured at the interval level
and normally distributed.
2)
Classical tests are built for the average respondents,
and do not measure high or low respondents very well.
3)
Statistics about test items depend on the respondent sample being
representative of population. It can only be confidently generalized to the
population from which the sample was drawn. As well as generalization beyond
that setting must be careful consideration.
4)
The test becomes longer, the more reliability.
5)
Researcher should not rely on previous reliability estimates of previous study.
It is suggested to estimate internal consistency for every study using the
sample obtained because estimates are sample dependent.
Read more about CTT as this link.
Item Response Theory (IRT)
The
item response theory (IRT) refers to a family of mathematical models that establishes
a link between the properties of items on an instrument, individuals responding
to these items, and the underlying trait being measured. IRT assumes that the
latent construct (e.g. stress, knowledge, attitudes) and items of a measure are
organized in an unobservable continuum. It focuses on establishing the
individual’s position on that continuum. IRT models can be divided into two families: unidimensional
and multidimensional. There
are a number of IRT models varying in the number of parameters (one, two and
three-parameter models), and non-parametric (Mokken scale).
IRT
Assumptions
The
purpose of IRT is to provide a framework for evaluating how well assessments
work, and how well individual items on assessments work.
1)
Monotonicity – The assumption indicates that as the trait level is
increasing, the probability of a correct response also increases.
2)
Unidimensionality – The model assumes that there is one dominant latent
trait being measured and that this trait is the driving force for the responses
observed for each item in the measure.
3)
Local Independence – Responses given to the separate items in a test are
mutually independent given a certain level of ability.
4)
Invariance – It is allowed to estimate the item parameters from any
position on the item response curve. Accordingly, we can estimate the
parameters of an item from any group of subjects who have answered the item.
Each
item on a test has its own characteristic curve that describes the probability
of getting each item right or wrong given the ability of the person.
Item
Response Function (IRF)
IRF is the relation between the respondent
differences on a construct and the probability of endorsing an item. The
response of a person to an item can be modeled by a mathematical item response
function (IRF).
Item
Characteristic Curve (ICC)
IRFs
can be converted into Item Characteristic Curve (ICC) which is graphic
functions that represent the respondent ability as a function of the
probability of endorsing the item. Depending on the IRT model used, these
curves indicate which items are more difficult and which items are better
discriminators of the attribute.

Item
Information Function (IIF)
Each
IRF can be transformed into an IIF. The information is an index representing
the item's ability to differentiate among individuals.
Discrimination
- height of the information (tall and narrow IIFs- large discrimination, short
and wide IIFs - low discrimination)
Test
Information Function
We
can judge the test as a whole and see at which part of the trait range it is
working the best.
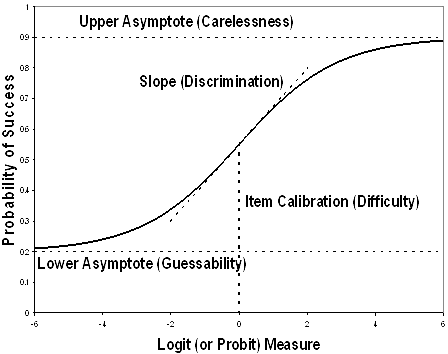
The
IRT mathematical model is defined by item parameters. Parameters on which items are characterized include their difficulty (b),
discrimination (a), and a pseudoguessing parameter (c).
-Location
(b): location on the difficulty range
"b"
is the item difficulty that determines the location of the IRF, an index of
what level of respondents for which the item is appropriate; typically ranges
from -3 to +3, with 0 being an average respondent level.
-Discrimination
(a): slope or correlation
"a"
is the item's discrimination that determines the steepness of the IRF, an index
of how well the item differentiates low from top respondents; typically ranges
from 0 to 2, where higher is better.
-Guessing
(c)
"c"
is a lower asymptote parameter for the IRF, typically is focus on 1/k
where k is the number of options. The inclusion of a "c" parameter
suggests that respondents with low trait level may still have a small
probability of endorsing an item.
-Upper
asymptote (d)
"d"
is an upper asymptote parameter for the IRF. The inclusion of a "d" parameter
suggests that respondents very high on the latent trait are not guaranteed to
endorse the item.
Advantages and Disadvantages of IRT
IRT provides flexibility in
situations where different sample or test forms are used. As
IRT model’s unit of analysis is the item, they can be used to compare items
from different measures provided that they are measuring the same latent
construct. Moreover, they can be used in differential item functioning, in
order to assess why items that are calibrated and test, still behave
differently among groups. Thus, that is allowed IRT findings are
foundation for computerized adaptive testing.
IRT models
are generally not sample- or test-dependents.
However, IRT are strict
assumptions, typically require large sample size (minimum 200; 1000 for complex
models), more difficult to use than CTT: IRT scoring generally requires relatively
complex estimation procedures, computer programs not readily
available and models are complex and difficult to understand.
Read
more about IRT as this link.
No comments:
Post a Comment